|
|
Se vuoi comunicare con Mario Della Penna: mariodellapenna@theorein.it
APPENDICE: IL FUZZY PENSIERO
Premessa
|
La spiccata attitudine in campo umanistico lasciava immaginare, in una prospettiva futura, scelte professionali ben specifiche in un genere di
attività inerente alle discipline letterarie.
Nonostante queste premesse, le necessità della vita mi hanno dirottato
in campi completamente "opposti".
Nel settore delle automazioni industriali, in cui lavoro, spesso mi trovo
a dover conciliare due mondi che da sempre sono visti alternativi: quello
umanistico e quello scientifico.
E’ parere di molti escludere ogni possibilità di dialogo fra queste
due sfere del sapere.
La mia esperienza nei due settori mi ha convinto del contrario: vi sono
molti più punti in comune di quante possano apparire le divergenze.
Questa appendice è dedicata proprio a questo tema e tenterò di farlo
attraverso un argomento molto specifico e di recente applicazione: si tratta
della logica fuzzy e del suo mondo circostante.
Questa logica ha la particolarità di non ridurre il suo campo di
applicazione alla semplice produzione di hardware e software nel settore
tecnologico, ma di inserirsi in un contesto molto più ampio, tanto che
esperti in materia, come ad esempio Burt Kosko, parlano di fuzzy pensiero.
Cercherò in queste poche pagine di illustrarne il contenuto ricorrendo
ad esemplificazioni di facile assimilazione. Origine del fuzzyIl passaggio dall’atomo al bit, come cita il titolo di questo lavoro, può dunque riferirsi a molteplici campi ed avere diversi angoli di lettura. Come ho cercato di mettere in evidenza, però, in qualsiasi settore applichiamo le nostre ricerche, tutto sembra ruotare attorno ad un approccio di tipo dualistico. L’uomo, pur essendo dotato di una potenzialità intellettiva molto complessa ed articolata, tende sempre a semplificare il prodotto dei suoi ragionamenti ammettendo solo due posizioni antitetiche. Il settore in cui tale atteggiamento consta di maggiori applicazioni è certamente quello relativo al campo scientifico. Si tratta di una prerogativa che sembra riguardare solo noi occidentali e la sua radice ha origini antiche; tuttavia non è difficile estrapolare fra i tanti padri di tale pensiero i due principali artefici: Aristotele e Descartes. Al grande pensatore francese si ricollegano tutti i successivi sviluppi tecno-scientifici dell’epoca moderna, ma paradossalmente, proprio il propulsore del pensiero dualistico è stato colui che, inconsapevolmente, può aver fornito elementi di riflessione per la nascita del pensiero fuzzy. Priva di provare a sostenere questa ipotesi è bene mettere in chiaro alcuni aspetti. La logica fuzzy ha un'origine molto recente. Il suo principio afferma che tutto è questione di misura. La qualità di ciò che è fuzzy ha un nome formalmente scientifico ed è quello di polivalenza. L’opposto di fuzzy è la bivalenza o due valori, due modi per rispondere a ogni domanda: vero o falso, 1 o 0. Quantità fuzzy vuol dire dunque polivalenza, ossia tre o più opzioni invece delle due sole alternative estreme. Significa inoltre analogico invece di binario, cioè infiniti gradi di grigio fra il bianco e il nero. Il principio implica che noi abbiamo in effetti a che fare con una logica a tre valori: enunciati veri, falsi o indeterminati. Il logico polacco Jan Lukasiewicz fu il primo a cimentarsi in questo nuovo mondo supponendo che l’indeterminazione definisse un continuum tra uno spettro di falsità e di verità. Fino ad allora logici come Bertrand Russell avevano usato il termine "vaghezza" (vagueness) per descrivere la polivalenza. Nel 1937 il filosofo Max Black pubblicò un saggio sugli insiemi vaghi ma il mondo della scienza e della filosofia ignorò il suo scritto. Nel 1965 Lotfi A. Zadeh, allora preside del dipartimento di ingegneria elettrica, mentre lavorava presso la Berkeley University pubblicò una relazione in cui venivano delineate le basi della teoria degli insiemi fuzzy (fuzzy sets). Quando fu introdotta per la prima volta essa si scontrò contro un muro di indifferenza e di ostilità e l’accoglienza ad essa riservata da parte di molti scienziati fu decisamente fredda. Tuttavia, negli anni Settanta del secolo appena trascorso, parecchi ricercatori europei, giapponesi e cinesi, iniziarono ad accorgersi delle sue potenzialità e a rendere disponibili i primi risultati concreti. L’introduzione di questa nuova logica segnava senz’altro l’inizio di una nuova era. Essa infatti non rappresentava l’estensione di concetti precedenti ma andava al di là di questi. La logica fuzzy è un concetto in sintonia con il modo di pensare degli esseri umani. Il principio fuzzy emerge da quasi tremila anni di cultura occidentale, da tremila anni di tentativi di negarlo, ignorarlo, confutarlo, etichettarlo in maniera mistificante e dichiararlo inesistente per definizione. Ma nonostante tutto, il nostro modo di ragionare, rimane fuzzy. Che ne sapeva Aristotele dei pomodori rossi?Prendiamo in mano una mela. E' una mela? Si. L'oggetto nelle nostre mani appartiene agli agglomerati spazio-temporali che chiamiamo l'insieme delle mele - di tutte le mele di ogni tempo e luogo. Ora stacchiamone un boccone, mastichiamolo e inghiottiamolo. Lasciamo che il nostro apparato digerente separi le molecole della mela. L'oggetto che abbiamo in mano è ancora una mela? O no? Stacchiamone un altro boccone. L'oggetto è ancora una mela? Diamo ancora un altro morso, e così via fino a finirla. La mela è mutata da una cosa in una non-cosa, in nulla. Ma dove abbiamo oltrepassato la linea di demarcazione fra mela e non-mela? Quando ne teniamo in mano metà, questa è tanto mela quanto non-mela. La mezza mela mette in crisi le descrizioni in termini di tutto-o-niente, è una mela fuzzy, è il grigio o chiaroscuro fra il bianco e il nero: il fuzzy è il chiaroscuro.
Un sera Renè Descartes (Cartesio) meditava davanti al camino su di un pezzo di cera. Egli pose in discussione la conoscenza sensibile ove questa voglia pretendere di essere l'unica fonte di conoscenza, mettendo così in luce come al di là del dato vi sono delle inferenze. Il filosofo prese spunto considerando le cose più comuni, e cioè partendo dai corpi che tocchiamo e vediamo, e che noi crediamo di comprendere nel modo più distinto. L’esempio di un pezzo di cera si prestava a chiarire questo suo concetto. Il suo colore, la sua figura, la sua grandezza erano manifesti, ma avvicinandolo ad una fonte di calore, ecco che vide perdere tutte le sue caratteristiche. Che cosa è, dunque, ciò che si conosceva con tanta distinzione in questo pezzo di cera? E’ l’interrogativo di fondo che si pose Descartes: "Donde quasi
concluderei che si conosce la cera per mezzo della visione degli occhi, e
non per la sola ispezione dello spirito (...) tuttavia, che vedo io da
questa finestra, se non dei cappelli e dei mantelli che potrebbero coprir
degli spettri o degli uomini finti, mossi solo per mezzo di molle? Ma io
giudico che sono veri uomini, e così comprendere per mezzo della sola
facoltà di giudicare, che risiede nel mio spirito, ciò che credevo di
vedere con i miei occhi".
Non possiamo quindi parlare di conoscenza se non c'è alla fine un atto
conoscitivo dell'intelligenza.
Dov'era andata a finire la cera? Ci troviamo di fronte alle stesse
domande ogni giorno guardandoci allo specchio.
Tutto muta impercettibilmente, a livello molecolare, sotto il nostro
sguardo. Gli atomi si aggregano e si disaggregano un quark alla volta. E la
divisione della materia può proseguire fino alla monadi di Leibniz.
Tutt'intorno a noi le cose mutano la loro identità. Tutto è mutamento.
Tutto fluisce. L'universo si sviluppa come un fiume che scorre. Gli atomi
delle punte delle nostre dita si avvolgono agli atomi dell'aria. Il
linguaggio fissa un legame fra una parola e la cosa significata. Il mondo
delle parole ben presto appare come un peschereccio che va alla deriva con
migliaia di lenze ingarbugliate o spezzate.
Percepiamo che le cose cambiamo eppure gran parte della scienza, della
matematica, della logica e della cultura muove dall'assunto di un mondo
stabile di cose assolutamente bianche o nere: ogni asserzione è o vera o
falsa.
La fede in questo presupposto dicotomico, questa ambivalenza, in
Occidente risale almeno agli antichi greci.
Democrito riduce l'universo ad atomi e vuoto. Platone riempie il suo
mondo di forme pure - del rosso, del giusto, della triangolarità e così
via. Aristotele spese una parte del suo tempo in quelle che ritenne fossero
le leggi dicotomiche della logica. La sua logica binaria si riduce a una
sola legge: A o non-A.
Per più di duemila anni la "legge" di Aristotele è stata il
parametro di ciò che era filosoficamente corretto. Ciononostante la fede
binaria ha sempre sollevato dubbi.
Il primo passo del suo sistema dottrinale Buddha, vissuto in India due
secoli prima di Aristotele, fu quello di sfondare il mondo verbale delle
alternative "o bianco o nero".
Questo tema del "chiaroscuro" è riscontrabile nei sistemi
dottrinali orientali vecchi e nuovi dal taoismo di Lao Tze al moderno Zen
del Giappone.
Un giorno Platone definì l'uomo un bipede implume e il giorno dopo uno
studente sofista entro in classe e gli offrì un pollo spennato.
Zenone raccolse un granello di sabbia da un mucchio e chiese se il
mucchio era ancora un mucchi.
Il mentitore di Creta diceva che tutti i cretesi erano mentitori e
chiedeva se aveva mentito.
Il logico Bertrand Russell scoprì il paradosso del mentitore di Creta
nei fondamenti della matematica moderna.
Anche Einstein aveva riflettuto sul "chiaroscuro", criticando
il positivismo logico.
L'enunciato logico "due è uguale a due" e l'enunciato
matematico "2+2=4" sono precisi e veri al 100%, come dicono i
filosofi "in tutti gli universi possibili", anche se ne hanno
visto solo uno.
Non potremmo mai dimostrare che sono veri al 100% enunciati come "la
luna brilla", "l'erba del prato è verde".
Le leggi della scienza non sono affatto leggi. Semplicemente fissano
tendenze osservate nel nostro angolo di universo. Ogni "legge"
della scienza può cambiare da un istante all'altro.
Per contro, il linguaggio della scienza, della matematica, della logica e
della programmazione informatica è strutturato secondo la dicotomia
"bianco o nero".
I filosofi sono partiti dal presupposto che il mondo sia assolutamente
bianco o nero, bivalente, proprio come il linguaggio e la matematica che
usano per descriverlo.
Dopo tutti questi anni e tanto filosofare prendono ancora ordini da
Aristotele senza discuterli.
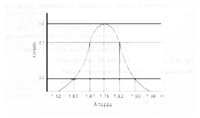
In realtà la logica fuzzy comincia dove finisce la logica occidentale. Interpretare i concetti di peso e di altezza con la logica fuzzyPrima dell'avvento del fuzzy, i concetti di "peso normale" e "altezza normale" erano difficilmente traducibili in informazioni gestibili da un normale elaboratore poiché trattasi di concetti imprecisi. Si supponga che un valore di altezza normale ragionevole sia 1,75 metri. Si può osservare che prendendo in esame una scala di altezze ordinata per valori crescenti, la percezione che si ha di altezza normale diviene via via più forte e va poi gradatamente scemando nel momento in cui si procede verso altezze sempre maggiori. Se si assegna un valore compreso tra 0 e 1 a questa percezione, ne risulta una curva come quella tracciata nella figura 1, che rappresenta una campana con un picco in corrispondenza del valore 1,75.
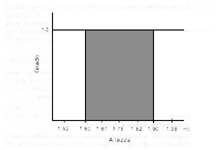
La funzione a campana viene definita funzione di appartenenza (membership function). Per un insieme fuzzy, l’altezza di ogni punto della curvatura, ovvero il grado, corrisponde all’intensità della nostra percezione relativamente al concetto di altezza normale, con un picco (massimo grado di intensità) che ha valore unitario. I punti che costituiscono la funzione di appartenenza possono assumere qualsiasi valore compreso tra 0 e 1. In questo modo risulta possibile avere un’idea quantitativa di un concetto di per sé inesatto oppure espresso in maniera ambigua. Osservando la figura 2, anche in questo caso è possibile disegnare un grafico con i gradi corrispondenti alle varie altezze. Infatti, nel caso il concetto di altezza normale venga espresso per mezzo di un insieme nettamente definito, il risultato è rappresentato da un grafico come quello evidenziato in figura, dove gli unici valori possibili sono 0 e 1.
In base a questo grafico, tutte le persone di altezza compresa tra 1,60 e 1,90 sono contraddistinte da un grado uguale a 1, così da rientrare nella categoria di persone di altezza normale. Tutte le persone di altezza inferiore a 1,60 e superiore a 1,90 sono invece caratterizzate da un grado pari a 0, per cui rientrano nella categoria di persona di altezza non normale. Chiaramente, una situazione come quella appena delineata non corrisponde alla realtà. Questa inaturalezza è dovuta al fatto che il procedimento binario non ammette l’esistenza di valori intermedi, ma costringe a passare da un insieme all’altro attraverso confini nettamente delineati. L’approccio che fa ricorso al set fuzzy e alle funzioni di appartenenza permette di far fronte in modo adeguato all’ambiguità precedentemente delineata e si superare l’imprecisione e la scarsa aderenza alla realtà insista negli insiemi nettamente definiti. Al fine di dimostrare che cosa si intende per logica si fa spesso ricorso ad un esempio classico. Generalmente sono i tre passi fondamentali che caratterizzano un’asserzione logica e possiamo vederli qui di seguito:
Si consideri adesso un altro esempio questa volta relativo alla logica fuzzy:
Con il termine fatto si intende qualcosa che è stato percepito e verificato mentre la conoscenza funge da tramite tra il fatto e la conclusione. A questo punto viene spontaneo chiedersi quale sia la differenza tra questi due tipi di logica. Nell’esempio precedente, l’essere umano citato nella riga in cui viene riportato il fatto e quello segnalato nella riga in cui è riportata la conclusione, è lo stesso. La medesima cosa avviene per il concetto di morte. L’esempio sulla logica formulato da Socrate si fonda sul fatto che i concetti cui si fa riferimento sono identici e possono venire espressi in modo preciso. Nel caso Socrate avesse fatto la seguente affermazione: "Socrate è parzialmente umano", esso non sarebbe potuto venire alla conclusone a cui è arrivato, ma la conclusione sarebbe stata di questo tenore: "Socrate morirà parzialmente". Questo rigore caratterizza il ragionamento binario ed è solitamente considerato un pregio. Tuttavia, le capacità sensoriali di cui sono dotati gli esseri umani danno risultati più precisi rispetto a quelli ottenibili nel caso binario e, sovente, anche più esatti. Nell’esempio della logica fuzzy, in cui si fa riferimento al pomodoro, è intrinsecamente presente un ragionamento più articolato e strettamente correlato con la percezione umana. Il fatto viene espresso con la seguente frase: "Il pomodoro è leggermente rosso", è differente dal concetto espresso dalla frase "se è rosso..." riportata nella riga relativa alla nozione. Se il concetto "leggermente rosso" viene considerato all’interno di un sistema in cui le nozioni siano definite in senso rigoroso, ovvero in cui le sfumature non vengono a considerate, un pomodoro con questa caratteristica non rientrerebbe nella categoria dei pomodori rossi e potrebbe dunque essere di qualsiasi altro colore, ad esempio giallo. Nell’esempio relativo alla logica fuzzy la conclusione era: " il pomodoro è poco maturo". La relazione che intercorre tra i concetti "è poco maturo" e "è maturo" è la medesima che lega i concetti "è leggermente rosso" e "è rosso". Nonostante quanto è stato finora detto, non si può affermare che le conclusioni a cui si perviene mediante la logica fuzzy coincidano esattamente con l’intuizione e l’esperienza umana o con la realtà. Si può affermare però che, nello stesso momento in cui la logica fuzzy cerca di interpretare la soggettività umana, essa è conforme ai principi dettati dalla logica e dal "buon senso". Theorèin - Marzo 2003 |